Introduction
This article will comprise a list of tips, strategies and techniques, which QTS students can incorporate into their revision to ensure they’ve given themselves the best possible chance of success in their Numeracy Skills Test. The advice contained herein can be treated as a checklist by students to make sure they’ve left no stone unturned in their preparations.
The first seven items on my checklist emphasise your core maths skills. To stand any chance of success at QTS level you will need to make sure these skills are fully functional. One or two items from this list may appear at first glance to be digressionary or slightly off-topic where the QTS syllabus is concerned. Don’t be misled here. I assure you all of these skills are essential and absolutely fundamental to everything you do in maths. Anything less than complete mastery of items 1-7 will seriously jeopardise your chances of passing. However, that’s not to say it will be enough for you to have excellent core skills alone. There are still specific topics you need to learn for your QTS test as well as specific skills and tactics you will need to deploy. So it’s one thing to have good all-round numeracy and quite another to have the added knowledge, methods and techniques needed to pass the test.
This is where checklist items 8 – 25 come in. Here, I have included additional, tailor-made advice and techniques (along with worked examples demonstrating the application of some of these techniques) which could, in theory, prove the difference between a pass and a fail on your numeracy test. Items 8 – 25 are more about putting the icing on the cake, so the first seven pointers on my checklist should still be your top priority. Good core skills may not be enough in isolation (i.e. without you adding the so-called ‘icing’), but any attempt to pass your QTS without good knowledge of these core skills is almost certainly doomed to failure.
Checklist
Core Skills Checklist
1) Fractions, Decimals and Percentages (F D P)
Know the rules for converting between any two from three of the above, and practice plenty of examples so you can do your conversions accurately and with speed. There are six permutations of conversions possible and you must be proficient in all six. I have listed them below:
F => D
D => F
F => P
P => F
D => P
P => D
Fractions, Decimals and Percentages are the three principal numerical formats we have available to us when representing quantities or proportions. Fractions, Decimals and Percentages are really just different ways of stating the same thing. The only reason why we might favour 1/2 ahead of 0.5 or 75% ahead of 3/4 is because one format may be better suited to a particular context. However, the distinction is a trivial one determined only by convention, so to all intents and purposes 1/2 = 0.5 = 50%
2) Know how to add, subtract, multiply and divide with fractions.
3) Be able to quickly calculate a fraction of a quantity.
This means multiplying the given quantity or number by a given fraction. The rule is: ‘Divide by the bottom; multiply by the top.”
Alternatively, if it’s easier to multiply the number by the top of the fraction first (i.e. the numerator), then by all means do this step first and divide by the bottom (denominator) second.
For example, (2/3) of 15 means (2/3) x 15 and is given by (15 ÷ 3) x 2 = 5 x 2 = 10
4) For fractions which appear in the test on a regular basis, you will be expected to know their conversions in an instant. I would therefore suggest that you commit to memory the corresponding decimals and percentages for the fractions you’re likely to encounter frequently.
I have included a list of these fractions with their associated conversions below:
1/2 = 0.5 = 50%
1/3 = 0.33 (to 2 d.p.) = 33.33% (to 2 d.p.)
1/4 = 0.25 = 25%
1/5 = 0.2 = 20%
1/8 = 0.125 = 12.5%
1/10 = 0.1 = 10%
1/20 = 0.05 = 5%
1/50 = 0.02 = 2%
1/100 = 0.01 = 1%
IMPORTANT: You should also know the corresponding decimals for the integer-multiples of these fractions. As an example, let’s look at multiples of 1/8:
1/8 = 0.125 = 12.5%
2/8 = 0.25 = 25%
3/8 = 0.375 = 37.5%
4/8 = 0.5 = 50%
5/8 = 0.625 = 62.5%
6/8 = 0.75 = 75%
7/8 = 0.875 = 87.5%
5) When your calculations involve fractions, a good habit to develop is to simplify the fraction(s) before you perform the calculation.
Example: (24/30) x 20 should first be rewritten as (4/5) x 20 to make the calculation much easier. Then you have (20 ÷ 5) x 4 = 16.
Be careful here, however, because there are times when simplifying is a bit of a false economy. A good example of this would be where you have to convert to a percentage a fraction such as 20/25, i.e. a fraction which has 25 in the denominator.
(20/25) x 100 is just as easily worked out in its raw state as (100 ÷ 25) x 20 = 4 x 20 = 80%. So in this case, there really is no need to first rewrite 20/25 as 4/5.
6) Practice your long multiplication and long division and make sure you know how to multiply non-integers containing decimal points.
When multiplying non-integers, ignore all decimal points to begin with and treat the
numbers you’re multiplying as if they were whole numbers. When you have done this calculation, you then reintroduce the decimal point into your answer.
Example: For 0.05 x 12, first consider 5 x 12, which is 60. Then reintroduce your decimal point two places in from the end to get 0.6. The same approach can be used to determine that 0.05 x 1.2 must be equal to 0.06.
When dividing by non-integers, I personally prefer to always convert the problem to one in which I’m working with whole numbers only. As with most things, this is best explained by way of an example:
1/0.4 = 10/4 (multiplying top and bottom by 10) and 10/4 = 2 and ½, or just 2.5
7) Know how to evaluate your answers to a given number of decimal places or a given number of significant figures.
QTS-specific Checklist
All examples referenced with page and question numbers have been taken from the fifth edition of Mark Patmore’s QTS book entitled ‘Passing the Numeracy Skills Test’.
Mental Arithmetic Checklist (first 12 questions of the QTS test)
8) Know thy times-tables.
This will not only help you to find the product of two numbers but also to find the answer to one number divided by another, e.g. 63 ÷ 7 = 9 is much easier to infer when you know your nine and seven times tables and can recall instantly that seven nines are sixty-three. So make sure you know your times-tables all the way up to 12 x 12.
9) To quickly work out the percentage of a number, first work out 10%, 5% or 1% of the number – whichever suits the purpose. Then you can scale up your answer by the relevant factor to get to the percentage you need.
Example 1: To work out 40% of 120, first find 10% by dividing 120 by 10 to get 12. Since 40% is four times as much as 10%, 40% of 120 = 4 x 12 = 48.
Example 2: To work out 35% of 120, first find 5% by dividing 120 by 10 and then halving 12 to get 6. Since 35% is seven times as much as 5%, 35% of 120 = 7 x 6 = 42.
10) To divide a number by 4, divide it by 2 twice in succession.
Example: 140/4 = (140 ÷ 2) ÷ 2 = 70 ÷ 2 = 35
11) Multiplying by 25 is the same as multiplying by the fraction 100/4, so you can divide by 4 first and then multiply by 100.
Example: 16 x 25 = (16 ÷ 4) x 100 = 400
12) Multiplying by 50 is the same as multiplying by the fraction 100/2, so you can halve your number first and then multiply by 100.
Example: 38 x 50 = (38 ÷ 2) x 100 = 19 x 100 = 1900
13) Dividing by a fraction is the same as multiplying by its reciprocal. Using general notation, this means that dividing by a/b is the same as multiplying by b/a.
Example: 4 ÷ (2/3) = 4 x (3/2) = 6
14) Conversions: For miles to kilometres, multiply by 8/5 and for kilometres to miles, divide by 8/5.
Example 1: Convert 20 miles to kilometres.
20 x 8/5 = 32km.
Example 2: Convert 32km to miles.
32 ÷ (8/5) = 32 x (5/8) = 20 miles
15) Dividing by 500 is the same as multiplying by the fraction 1/500 or 2/1000, so you can divide your number by 1000 first and then multiply by 2.
Example: 1283 ÷ 500 = (1283 ÷ 1000) x 2 = 1.283 x 2 = 2.566
16) When dividing larger numbers, it’s often easier to simplify the equivalent fraction. To simplify any fraction, you divide top and bottom repeatedly by common factors.
Example: Dividing 600 by 8 is the same as simplifying and then evaluating the fraction 600/8. In this case, you can halve top and bottom repeatedly as follows: 600/8 = 300/4 = 150/2 = 75
We can apply this tactic to question 8 on page 14 of the QTS Book.:
It is possible to seat forty people in a row across the hall. How many rows are needed to seat four hundred and thirty-two people?
432/40 = 216/20 = 108/10 = 10.8. Therefore, 11 rows are needed.
Alternatively, you can keep 432/40 in its raw state and convert it to a mixed number and fraction by noting that 432/40 is simply 10 and 32/40 or 11 when rounded up, as is required.
17) When working out the product of a series of large numbers, you can simplify matters by factoring the numbers you’re multiplying and utilising the fact that multiplication is commutative (i.e. can be executed in any order).
Example: Question 12 on page 14 of the QTS Book:
Two hundred pupils correctly completed a sponsored spell of fifty words. Each pupil was sponsored at five pence per word. How much money did the pupils raise in total?
200 x 50 x 5 = 2 x 5 x 5 x 100 x 10 = 50 x 1000 = 50,000p or £500.00
18) Make sure you can multiply single-digit numbers by double-digit numbers with speed and accuracy.
Example: 8 x 34 = (8 x 30) + (8 x 4) = 240 + 32 = 272, i.e. eight thirties plus eight fours.
19) Subtracting a given fraction from one is the same as finding the difference between the fraction in question and one whole. In other words, if I want to subtract two-fifths from one, I need only ask myself how many fifths I have to add to two-fifths in order to get five-fifths (five-fifths is just another way of saying one). Adding three-fifths to two-fifths gives me five-fifths (i.e. one whole), so 1 – 2/5 = 3/5.
The general formula for taking away any fraction a/b from one is given below:
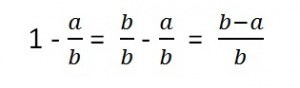Let’s take a look at a few examples:
We can now apply this method to question 16 on page 14.
In a class of thirty-five pupils, four out of seven are boys. How many girls are there in the class?
Firstly, the fraction of the class which is girls is given by 1 – 4/7 = (7/7) – (4/7) = 3/7. The number of girls in the class is then given by (3/7) x 35 = (35 ÷ 7) x 3 = 5 x 3 = 15
20) Know your multiples of sixty so that you can quickly convert ‘minutes’ to ‘hours and minutes’.
1, 2, 3, 4 and 5 hours equate to 60, 120, 180, 240 and 300 minutes respectively. Knowing this makes conversions such as 315 minutes = 5 hours and 15 minutes much quicker to perform.
21) If a teacher needs to interview, without overlap, x pupils and each pupil is allocated y minutes, then the minimum number of z-minute appointment slots required is given by the general formula:
No. of z-minute appointment slots = x ÷ (z ÷ y), where z ÷ y is first rounded down to the nearest integer before being plugged into the formula. Your calculation for x ÷ (z ÷ y) then has to be rounded up.
Example: Question 20 on page 14 of the QTS Book.
A teacher needs to interview forty pupils for their Record of Achievement. Each pupil is allocated eight minutes. What is the minimum number of half-hour lessons needed to carry out all of the interviews? Interviews must not overlap lessons.
No. of 30-minute appointment slots = 40 ÷ (30 ÷ 8), where 30 ÷ 8 is first rounded down to the nearest integer to give 3 before being plugged into the formula. Your calculation then becomes 40 ÷ 3, which then has to be rounded up. 40/3 = 13 and 1/3. Therefore, 14 half-hour lessons are needed to carry out all of the interviews.
General pointers
22) When answering the mental arithmetic questions, aim to be as economical as you can with your written workings.
The less ink you shed on the page and the more working out you can do mentally without compromising accuracy, then the less time you will use up, and subsequently, the less pressure you will feel under to submit your answers in time.
Remember, you don’t need to write down every step of your working as many of the steps can be done just as easily in your head. Take question 2 on page 13, for example:
A test has forty questions, each worth one mark. The pass mark was seventy percent. How many questions had to be answered correctly to pass the test?
Simply jot down 40 and 70% and then write your answer 28. The long-hand step-by-step method would be as follows:
70% of 40 = (70/100) x 40 = (7/10) x 40 = (40 ÷ 10) x 7 = 4 x 7 = 28%
However, notice how much quicker it is to work out mentally that 10% of 40 is 4 and 70% must be seven times as much to give 28. So all you really need to write down is 40, 70% and your answer, 28.
23) Do as many distinct practice tests of twenty-eight questions as you can and use a grid format to index each question, highlighting those which need extra practice.
Let’s say you manage to source eight practice tests of twenty-eight questions. You should use a spreadsheet to index all 224 of these questions in an 8 x 28 grid. Tick off those questions you feel you’ve mastered and highlight those which you feel need extra work. Then practice your weaker questions over and over again until those too have been mastered.
24) Make sure you’re one hundred percent on all your practice questions before the test. Dedicate yourself to your revision as if you can expect your actual test score to be as much as twenty percent less than the minimum score you’re achieving in practice.
This projection of a twenty percent reduction from practice-to-actual might be overly pessimistic, but it can be a good thing to be pessimistic about your projections if it strengthens your resolve in practice. Such a reduction might be anticipated due to any number of factors such as lapses in concentration, basic ‘kick-yourself-type’ arithmetical errors, nerves, seemingly tougher-than-normal type questions, and so on.
However, take comfort in the fact that, for a pass, you need only eighteen questions right out of twenty eight. This equates to 64.3% rounded to one decimal place. So if you’re one hundred percent in practice, and can expect at worst eighty percent in your actual test, then you’ll be fine. In fact, if you’re consistently scoring twenty-five out of twenty-eight in practice you should still be good for at least twenty answers correct on the actual test and therefore “good to go”.
You should make plans as if fate was conspiring to deliver you the toughest test conceivable for the QTS. Be pessimistic about your expectations for the level of difficulty you’ll face on the day. Don’t be the optimist who drowned in a half-full bath tub! By all means, be positive and confident when it comes to your mental state, but be a pessimist when it comes to your expectations about actual test questions. If you make your plans for the worst-case scenario, things will go all the more smoother for you on the day.
25) My final tip is this: Give yourself enough time on test day to complete a final set of fully twenty eight practice questions just before you sit the actual test.
This will ensure you’re not entering the actual test cold, so to speak. You now have all the skills and knowledge you need, but anyone can get caught off-guard if not properly warmed up. The brain works more efficiently when it’s warmed up properly, so before you even sit the test, make sure you find your rhythm and those all-important mental grooves that worked so well for you in practice. Don’t let your first warm up session be the first few questions of the actual test. You’ll quickly warm up as the test progresses in any case, but why delay warming up until the official test starts and risk being caught cold?
So complete a practice test as close to the actual test as you can and give yourself every chance to hit the ground running!
One-to-one Personal QTS Tuition
For one-to-one mentoring support on the numeracy side of the QTS test, please take a look at my Maths Tutoring Services page where I have provided you with various options for contacting me in case you would like to book some lessons.
